Calculateur d'intérêts composés
Les intérêts composés sont un concept fondamental en finance et en investissement. Ils jouent un rôle clé dans la croissance de la richesse à long terme.
Ce concept repose sur l'idée que non seulement le capital initial génère des intérêts, mais que les intérêts eux-mêmes génèrent également des intérêts.
Calculer un intêret composé
Qu'est-ce que les intérêts composés ?
Les intérêts composés désignent les intérêts accumulés sur un capital initial et sur les intérêts précédemment gagnés. Contrairement aux intérêts simples, où les intérêts ne sont calculés que sur le capital initial, les intérêts composés réinvestissent les intérêts dans le capital.
En conséquence, la somme d'argent augmente plus rapidement, surtout si le processus est répété sur une longue période.
En d'autres termes, c'est comme un effet boule de neige : plus le capital augmente avec le temps, plus les intérêts générés sur ce capital seront importants.
Importance des intérêts composés
Les intérêts composés sont particulièrement bénéfiques pour les investissements à long terme, car ils permettent une croissance exponentielle des fonds.
Plus longtemps vous laissez votre capital travailler avec des intérêts composés, plus vous accumulerez d'argent, même si le taux d'intérêt semble faible au départ. Cette approche est couramment utilisée dans les comptes d'épargne, les fonds de retraite, et bien d'autres produits financiers.
La formule des intérêts composés
Pour calculer les intérêts composés, il existe une formule mathématique relativement simple que vous pouvez utiliser.
La formule de base est la suivante :
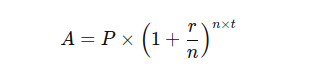
Où :
- A représente le montant total après capitalisation (la valeur future).
- P est le montant initial investi (le principal).
- r est le taux d'intérêt annuel sous forme décimale (par exemple, 5 % devient 0,05).
- n est le nombre de fois que les intérêts sont composés par an (par exemple, 12 pour une composition mensuelle).
- t est la durée de l'investissement en années.
Explication des variables :
- Capital initial (P) : Il s'agit de la somme que vous investissez au départ.
- Taux d'intérêt annuel (r) : Ce taux représente le rendement de l'investissement sous forme de pourcentage.
- Nombre de périodes de composition par an (n) : Il est essentiel de savoir à quelle fréquence les intérêts sont ajoutés au capital. Les compositions peuvent être annuelles, semestrielles, trimestrielles, mensuelles, voire journalières.
- Durée de l'investissement (t) : Plus vous laissez votre argent travailler longtemps, plus les intérêts seront composés et plus votre capital augmentera rapidement.
Exemple de calcul des intérêts composés
Prenons un exemple simple pour illustrer la puissance des intérêts composés.
Supposons que vous investissiez 1 000 € dans un compte d'épargne offrant un taux d'intérêt annuel de 5 %, avec une composition annuelle des intérêts, pendant 5 ans.
Étape 1 : Appliquer la formule
Ici :
- P = 1 000 €
- r = 0,05
- n = 1 (composition annuelle)
- t = 5 ans
La formule devient :
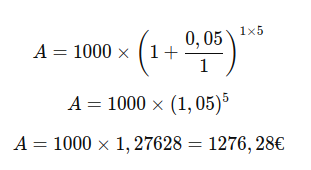
Ainsi, après 5 ans, votre investissement vaudra 1 276,28 €, soit 276,28 € d'intérêts gagnés sur 5 ans.
Exemple avec une composition mensuelle
Si les intérêts étaient composés mensuellement, le calcul changerait légèrement. n = 12 (pour une composition mensuelle)
La nouvelle formule devient :
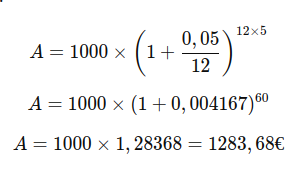
Avec une composition mensuelle, l'investissement vaudrait 1 283,68 € après 5 ans, ce qui génère des intérêts légèrement plus élevés que dans le cas de la composition annuelle.
Le facteur temps et la croissance exponentielle
L'une des caractéristiques les plus puissantes des intérêts composés est la croissance exponentielle. Plus le temps passe, plus le capital augmente rapidement.
Voici un exemple pour illustrer cela.
Supposons que vous investissiez 1 000 € au taux de 5 % et que vous laissiez cet argent sans y toucher pendant différentes périodes, avec une composition annuelle.
- Après 10 ans, l'investissement vaudra 1 628,89 €.
- Après 20 ans, il vaudra 2 653,30 €.
- Après 30 ans, il atteindra 4 321,94 €.
Cela montre à quel point l'effet des intérêts composés s'accélère avec le temps. Après 30 ans, la valeur de l'investissement est plus de quatre fois son montant initial, simplement en laissant les intérêts se composer année après année.
L'effet de la fréquence de composition
Plus les intérêts sont composés fréquemment, plus le montant final sera élevé. Par exemple, si les intérêts sont composés annuellement, le montant des intérêts sera plus faible que si les intérêts sont composés mensuellement, trimestriellement ou même quotidiennement.
Prenons un exemple pour illustrer cet effet :
- Capital initial : 1 000 €
- Taux d'intérêt annuel : 5 %
- Durée : 10 ans
| Fréquence de composition | Montant final (A) |
|---|---|
| Annuellement | 1 628,89 € |
| Semestriellement | 1 645,31 € |
| Trimestriellement | 1 653,29 € |
| Mensuellement | 1 647,01 € |
| Quotidiennement | 1 648,66 € |
Comme on peut le voir, plus la fréquence de composition des intérêts est élevée, plus le montant final sera important.