Comment calculer l'aire d'un triangle
Calculer l'aire d'un triangle est une compétence de base en mathématiques, utile aussi bien dans le cadre scolaire que dans de nombreux domaines de la vie courante, comme le design, la construction ou encore l'ingénierie. Ce guide détaillé vous expliquera les différentes méthodes de calcul de l'aire d'un triangle en fonction des informations dont vous disposez.
Formule de Base : L'Aire d'un Triangle avec la Base et la Hauteur
La formule la plus courante et la plus simple pour calculer l'aire d'un triangle nécessite de connaître la longueur de sa base et de sa hauteur.
La formule:
L'aire d'un triangle se calcule avec la formule suivante :
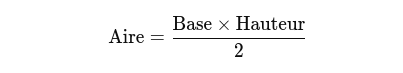
Exemple de Calcul
Supposons que la base d'un triangle mesure 10 cm et sa hauteur 5 cm :
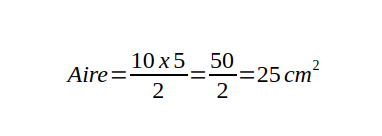
Calcul de l'Aire d'un Triangle en Utilisant les Longueurs des Côtés : La Formule de Héron
Lorsque vous connaissez les longueurs des trois côtés d'un triangle, mais pas la hauteur, la formule de Héron est idéale.
La formule de Héron:
1 - Calculez le demi-périmètre (p) du triangle :
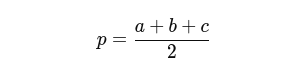
où (a), (b), et (c) sont les longueurs des trois côtés du triangle.
2 - Calculez l'aire avec la formule suivante :
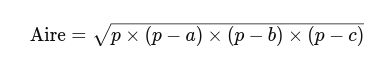
Exemple de Calcul
Imaginons un triangle avec des côtés de longueurs 7 cm, 8 cm, et 9 cm :
- Calculez le demi-périmètre :
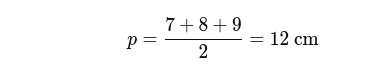
- Calculez l'aire :
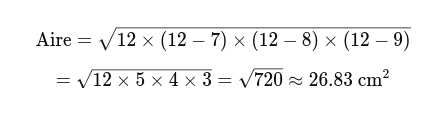
Calculer l'Aire d'un Triangle avec Deux Côtés et l'Angle Entre Eux
Lorsque vous connaissez deux côtés d'un triangle ainsi que l'angle entre eux, vous pouvez utiliser une formule trigonométrique.
La formule:
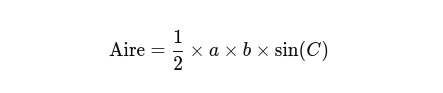
où (a) et (b) sont les longueurs des deux côtés, et (C) est la mesure de l'angle compris entre ces deux côtés.
Exemple de Calcul
Si vous avez un triangle avec des côtés de longueurs 8 cm et 6 cm, et un angle de 30° entre eux :
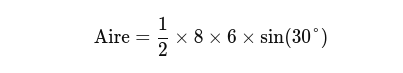
Sachant que sin(30°) = 0,5 :
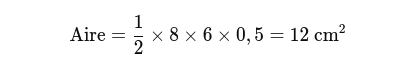
Cas Particuliers : Aire d'un Triangle Équilatéral
Pour un triangle équilatéral, où les trois côtés sont de même longueur, on peut utiliser une formule simplifiée. Si (a) représente la longueur de chaque côté, l'aire se calcule avec la formule suivante :
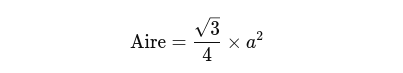
Exemple de Calcul
Pour un triangle équilatéral dont chaque côté mesure 6 cm :
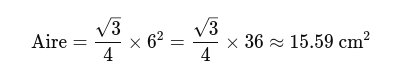
Questions Fréquentes
1. Pourquoi divise-t-on par deux dans la formule de base pour l’aire d’un triangle ?
Diviser par deux est nécessaire car un triangle est la moitié d’un parallélogramme avec la même base et la même hauteur.
2. La formule de Héron fonctionne-t-elle pour tous les types de triangles ?
Oui, la formule de Héron fonctionne pour tous les types de triangles, qu’ils soient scalènes, isocèles ou équilatéraux.
3. Comment utiliser une calculatrice pour appliquer la formule trigonométrique ?
Vérifiez que votre calculatrice est en mode degrés ou radians, selon la mesure de l'angle. Ensuite, entrez les valeurs dans l'ordre pour obtenir une aire précise.